SOLUCIÓN GEOMÉTRICA AL CÁLCULO DE LA ALTURA DE LA DERIVA EN CAMPOS CIRCULARES

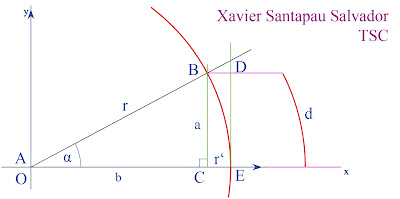
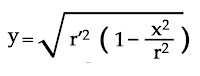Para el cálculo de la altura alcanzada por la deriva de la luz en campos circulares como el de la Vía Láctea nos valdremos de la función seno y del teorema de Pitágoras.

Los datos que conocemos son:

r = 95.000 años luz. (AB).

Pe Periodo = 240.000.000 años.

Pr Perímetro = 2·π·r = 596902,60 a l.

y buscamos:

α : Ángulo del triángulo

a : Altura del triangulo rectángulo (BC)

b : segundo cateto (OC)

r' : Altura de deriva (CE)

Para poder calcular el angulo α deberemos conocer d, que es el recorrido o el tiempo transcurrido durante el tiempo que tarda la luz en recorrer la distancia de su radio. De cualquiera de las dos maneras obtendremos el mismo resultado.

En tiempo 

d = t = 95.000 años. 

α = d · 360ᵒ / Pe = 95.000 · 360ᵒ / 240.000.000 = 0.1425ᵒ

En distancia

t =  95.000 años.

d = Pr . t / Pe

d = 596.902,60 · 95.000 / 240.000.000 = 236,27394 al.

α = d · 360ᵒ / Pe =  236,27394 al · 360ᵒ /  596.902,60 = 0.1425ᵒ

Una vez conocemos α calculamos la altura a del rectángulo a partir de la función seno y el radio r.

sen (α) = a / r = BC / AB

a =  sen(α) · r = sen(0.1425) · 95.000 = 236,2737039

y solo nos queda calcular finalmente b para completar el triangulo rectángulo.

b = 94.999,706184 al.

Una vez conocemos b, si observamos la circunferencia en movimiento, podemos deducir que r' será la sombra del recorrido curvo sobre el eje X, y que por el principio de proporcionalidad que he visto que se da en círculos y anillos en rotación entre los segmentos del arco definidos por la rotación dentro de un intervalo y la proyección sobre cada eje x-y, siendo en X, y a modo analógico al estilo espacial Katherine, la altura de puente de deriva que buscamos es (r'). También podemos derivar en función al tiempo y encontrar dicho dato, pero me gusta mas así, a la vieja usanza, sin derivadas, ejercitando la visión espacial. Dicho resultado (r'), nos sirve para calcular la deriva que experimentara un vector al cruzar una superficie circular en movimiento uniforme mediante el uso de la siguiente fórmula:

Ahora ya podemos calcular la altura de deriva restando b del radio r:

r' = r - b = 95.000 - 94.999,706184 = 0.293816 al.

Convertimos los años luz en Km...

0.293816 al · 9.460.730.472.580,8 Km = 2.779.713.984.531,8 Km.

A partir de aquí, ya podemos calcular la altura de deriva para cualquier punto del eje x.

Si la tierra está a 25.766 años luz del centro de la galaxia, la altura de deriva será en ella de 

y = 0,2828029

CÁLCULO DE LA DERIVA DE LA LUZ EN CAMPOS EN MOVIMIENTO

Para calcular cual sería la deriva que experimenta un rayo de luz en la Vía Láctea cuando se desplaza por el plano de la misma donde el campo tenfria un desplazamiento nos valdremos de la función:

A partir de ella, despejaremos la "y" para obtener cual ha sido la deriva de la luz a la altura en que se encuentra el observador.

Teniendo presente que r' es altura del puente que describe la trayectoria de la luz, será dicho dato junto con la velocidad de traslación lo que nos permitirá calcular la deriva para cualquier punto del plano de la galaxia.

r' = ((r) x (Vat/C))

DATOS:

Velocidad galaxia por el universo 555 Km/sg 

Diámetro: 190.000 años luz.

Radio: r = 95.000 años luz.

Grosor: 10.000 años luz.

Periodo de rotación 240.000.000 años

Vat: Velocidad angular Traslación en todo su radio exterior 220-240 Km/seg. (230 Km/seg de media).

C = 299.792,458 Km/seg.

Hemos de tener presente que la Vía Láctea no es homogénea y que la velocidad de traslación de la misma no es del tipo angular como ocurre en cualquier movimiento circular uniforme, sino que se desplaza en bloque en una amplia sección de su radio, lo que hace que la deriva tienda a ser más en diagonal que no circular dentro de dicho intervalo.

También hemos de tener presente que todos los datos son aproximados pues se desconoce la certeza exacta de estos.

Si sabemos que la distancia del sol al centro galáctico es de 25.766 años luz, y conocemos tambien los ràdios (r) y (r'), aplicando la formula podremos calculara la deriva de un rayo de luz que debería pasar por el centro de la circunferencia a la altura de nuestro Sol.

y = ? al.

En la próxima entrada les mostraré como calcular la altura del puente (r') de manera sencilla con un método que me he sacado de la manga.